Ci sono cose che sembrano impossibili e invece non lo sono: c'è sempre una soluzione. Un esempio è il paradosso del cuneo: la ridisposizione di una serie di tessere per semplice traslazione e rotazione sembra modificare la superficie totale delle tessere.
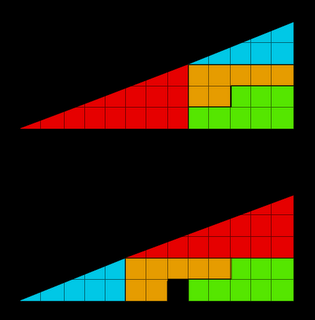
Le due figure sono composte dalle stesse tessere di uguale superficie, come si può constatare contando i quadrati della griglia. Due triangoli con base ed altezza identiche hanno la stessa area. Ci si trova nella situazione paradossale in cui la somma di quantità uguali dà risultati differenti.
Il paradosso viene a cadere quando si constata che le due figure rappresentate non sono triangoli ma quadrilateri. Il quarto angolo, quasi piatto, si trova su quella che si riteneva essere l'ipotenusa, tra la tessera azzurra e la tessera rossa. Utilizzando un righello si può constatare che nella prima costruzione l'angolo è leggermente maggiore di 180° e la figura è concava. Nella seconda disposizione l'angolo è minore di 180° e la figura è convessa. L'area pari alla differenza tra i due casi equivale all'area del quadrato vuoto.
Sembrava impossibile che un uomo proveniente dal PCI potesse arrivare fino al colle più alto di Roma e invece è caduto il "fattore K". L'elezione di Napolitano è il riconosciumento dell'importante contribuito della sinistra nella costruzione dell'Italia repubblicana: un segno di maturità della nostra società. Finalmente qualche buona notizia!
Nessun commento:
Posta un commento